문제
우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행사가 되어 새로운 세계에 발을 내려 놓는 영광의 순간을 기다리고 있다.
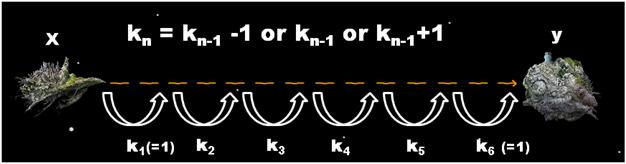
그가 탑승하게 될 우주선은 Alpha Centauri라는 새로운 인류의 보금자리를 개척하기 위한 대규모 생활 유지 시스템을 탑재하고 있기 때문에, 그 크기와 질량이 엄청난 이유로 최신기술력을 총 동원하여 개발한 공간이동 장치를 탑재하였다. 하지만 이 공간이동 장치는 이동 거리를 급격하게 늘릴 경우 기계에 심각한 결함이 발생하는 단점이 있어서, 이전 작동시기에 k광년을 이동하였을 때는 k-1 , k 혹은 k+1 광년만을 다시 이동할 수 있다.
예를 들어, 이 장치를 처음 작동시킬 경우 -1 , 0 , 1 광년을 이론상 이동할 수 있으나 사실상 음수 혹은 0 거리만큼의 이동은 의미가 없으므로 1 광년을 이동할 수 있으며, 그 다음에는 0 , 1 , 2 광년을 이동할 수 있는 것이다. ( 여기서 다시 2광년을 이동한다면 다음 시기엔 1, 2, 3 광년을 이동할 수 있다. )
김우현은 공간이동 장치 작동시의 에너지 소모가 크다는 점을 잘 알고 있기 때문에 x지점에서 y지점을 향해 최소한의 작동 횟수로 이동하려 한다. 하지만 y지점에 도착해서도 공간 이동장치의 안전성을 위하여 y지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.
김우현을 위해 x지점부터 정확히 y지점으로 이동하는데 필요한 공간 이동 장치 작동 횟수의 최솟값을 구하는 프로그램을 작성하라.
이 풀이는 시간초과가 발생하는 부분이니 더 내려가서 추가 부분을 봐주세요!
저는 반복문을 통해 x부터 y까지 가능한 이동 범위 중 가장 큰 k+1을 추가하되 도착 직전에 이동 범위가 1이 아닌 경우 이전으로 돌아가도록 코드를 작성하였습니다.
while (i < y) { // i: 현재 위치
k = termList.peek(); // 이전 이동 범위
term[0] = k + 1; // 가능한 이동 범위 세가지 모두 추출
term[1] = k;
term[2] = k - 1;
k = -1;
for (int tmp : term) { // 이동 범위 중 가능한 범위 추출 (큰 순으로)
if (i + tmp < y || (i+tmp == y && tmp ==1)) {
// y를 벗어나지 않거나 y 직전일 때 이동 거리가 1인 경우
k = tmp;
break;
}
}
if (k <= 0) { // 가능한 이동 범위가 없음
termList.add(termList.pop() - 1);
}else if(i+k == y && k != 1){ // 마지막 이동이 1이 아닌 경우
termList.add(termList.pop() - 1);
}else{ // 가능한 이동 범위인 경우 stack에 저장
i+=k;
location.add(i);
termList.add(k);
}
}
이전으로 돌아가기 위해 거쳐온 위치를 stack에 저장했습니다. 또 이동 범위도 같이 스택에 저장하였습니다.
끝으로는 이 stack의 size를 return하며 종료합니다.
근데 이 방법으로는 시간초과가 발생하네요…. 다시 풀어보고 추가하겠습니다!
추가 2021.02.13
제가 너무 로직이 아니라 순회에 꽂혀서 계속 시간 초과가 발생했어요! 위 문제를 업그레이드해서 앞, 뒤로 이동해서 거리를 구하는 방식을 써봤는데도 시간 초과되더라구요.. 질문게시판을 뒤지다가 우연히 발견한 글을 참고해서 겨우 풀 수 있었습니다.
토대로 정리해보았습니다.
1. 최대거리
사실 이 문제를 처음 봤을 때 대칭을 생각했었는데 대칭이 아닌 케이스도 있어 넘겼었는데 이게 힌트였네요!
| i | 거리 (y-x) | 이상적인 이동거리 목록 | 이동 횟수 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 4 | 121 | 3 |
| 3 | 9 | 12321 | 5 |
| 4 | 16 | 1234321 | 7 |
| 5 | 25 | 123454321 | 9 |
위 경우를 제외하곤 이상적인(대칭적인) 이동을 할 수 없어요! 반대로 저 경우들은 최대거리 이상의 거리를 갈 수 없습니다.
최대거리 이상으로 이동한다면 마지막 이동 거리가 1이 될 수 없다.
이동거리가 d일 때 d 제곱근 이하의 가장 큰 정수가 최대거리이다.
2. 이동 횟수
위처럼 이동거리 목록이 대칭을 이루는 경우엔 이동 횟수가 규칙적으로 증가합니다.
최대거리가 i일 때, 이동 횟수는 2 * i + 1 이상 이다.
보시면 알겠지만 중심을 기준으로 앞, 뒤에 횟수가 한 번씩 추가되어 이런 규칙을 띄는 것입니다.
위에서 2 * i + 1 이상이라고 한 이유는 이동거리 d가 nn < d < (n+1)(n+1) 인 경우에 추가적인 이동이 필요하기 때문입니다.
r = distance - i*i
최대거리 이하 이동거리는 한 번의 이동으로 이동할 수 있습니다. 거리 r을 가기위해 필요한 추가 이동은 r / 최대거리이고 r % 최대거리가 0이 아니면 1번의 추가적으로 이동이 필요합니다.
3. 최종 알고리즘
1. 최대거리 구하기 (distance의 제곱근 이하의 가장 큰 정수)
long maxSpeed = (long) Math.sqrt(distance);
2. 이동 횟수 구하기
answer = 2 * maxSpeed - 1;
r -= maxSpeed*maxSpeed;
answer += (r/maxSpeed);
if(r % maxSpeed != 0 ){
answer++;
}
4. 예시
x = 0 y = 13
- 최대거리: 3 (9 <= y < 16)
- 이동횟수: (2*3+1) + a
- r = 13 - 9 = 4일 때, r/3 = 1이고 r%3 > 0이니 두 번의 이동이 추가적으로 필요하다.
- 즉 7+2번의 이동 필요합니다.
- 이동거리 목록
- distance = 9일 때는 12321이고 13일 때는 최대거리 만큼의 이동과 r%3=1만큼의 이동을 추가해 1233211 입니다.
감사합니다.
참고한 게시글: https://www.acmicpc.net/board/view/13747
Text by Chaelin. Photographs by Baekjoon Online Judge.